並列計算のヒント: 浮動小数点計算の再現性を保つためのヒント

並列計算時の数値演算の再現性問題

計算機で浮動小数点演算を行う場合，一般にその結果は数学的な演算とは一致しない。たとえば，一般に計算機の加算のような浮動小数演算では次式のように結合法則が成立しない。

\[ (x + y) + z \stackrel{?}{=} x + (y + z)\]

10 進数で有限桁数な数でも 2 進数表記では有限桁数で正確に表現できない場合などもある。数学的に正確ではない例として，以下のように $0.1 + 0.01 - 0.1 - 0.01$ を計算すると $0$ にならない。(Python 3.8.5)

     >>> 0.1 + 0.01 - 0.1 - 0.01
     -5.204170427930421e-18

しかし，$0.1 - 0.1 + 0.01 - 0.01$ の結果は $0$ である。

     >>> 0.1 - 0.1 + 0.01 - 0.01
     0.0

また，絶対値の極端に違う数値の加減算で絶対値の小さな値が値に反映されないアンダーフロー問題などもある。これは丸めの演算が演算順序に依存する(Order dependent rounding) 問題である。大きな数に極端な小さな数を複数たす場合，丸めによって小さな数が皆無視される場合でも，小さな数を先にたすことで，無視されなくなる場合がある。

しかし，アルゴリズムの多くはある演算結果の等値性に依存する。そのためにこの数値演算の再現性は重要な問題となる。演算結果が等しくないという場合でもその差は最初の数値演算の例のようにかなり小さいことが普通なので，これをある範囲の上限と下限を記録する interval algorithm を使うことができる場合がある。ただし interval algorithm は今回の Tips では用いない。

今回の Tips では演算順序の違いによる問題を避けるために並列演算の各スレッドやプロセスで演算が同じ順序になるようにする方法例を述べる。

具体的問題例

具体例として以下の 2 つの幾何学問題を用いる。

•  空間分割型の ray-object intersection
•  3 角形メッシュにおける plane-triangle intersection

空間分割型の Ray-object intersection

図 1 に空間が 2 つの立方体で分割されていて，その境界にポリゴン (3 角形)が 1 つある状況を示す。この ray の交差点が丁度境界上に位置するとする。この計算は空間 s1 を担当するユニットと空間s2 を担当するユニットの 2 つが独立して並列におこなわれると仮定する。次式が ray の式とする。ここで，${\boldsymbol P_0}$ が視点，$\boldsymbol d$ が方向ベクトル，$t$ を ray のパラメータとする。
\[\boldsymbol{r}(t) &=& \boldsymbol{P}_0 + t \boldsymbol{d} \]

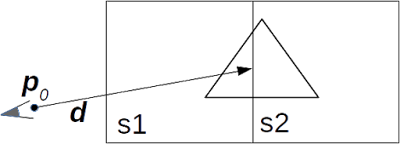Figure 1: Space subdivision ray-object intersection

ray の空間 traverse のために 3D-Digital Differential Analyser (3DDDA) を元にするアルゴリズムを使う場合，s1 で利用する式の $t$ と s2 で利用する式の $t$ が異なる。これは $t$ の値が ray が最初に部分空間に hit した値を使うのが通常だからである。空間分割を行い，計算を各部分空間ごとに独立して行う場合，2 つの部分空間でそれぞれの交差判定が行なわれる。この際の numericalreproducibility を確かなものにするために，この 2 つの計算の入力データを完全に同一にするように注意する。

同一とは浮動小数点のバイナリデータとして値が全ての bit で同一になるようにする。つまり normalization なども注意する。また，ポリゴンのデータが各計算要素のために複製される場合にはエッジの順番も保存する。単なる複製の場合にはこの順番が変更されることはないだろうが，もしポリゴンを各空間に収まるように分割する時には注意が必要である。

このような ray-object 交差で numerical reproducibility が問題になるのは，特に半透明の物体の場合である。もし ray parameter の $t$ が各空間で異なる場合，僅かな計算結果の違いがでるため，両方の部分空間で hit と判定された場合や，両方の部分空間で hit しないと判定された場合にポリゴン上に artifactが出ることになる。

部分空間の並列計算で numerical reproducibility の問題を避けるために 3DDDA を使うことはあきらめた。ray は常に originから $t$ を計算する。空間分割の境界の位置はどの空間でも同一の入力から計算し，incremental の計算は行わないことでどの空間でも同一の浮動小数点表現を得るようにする。

3 角形メッシュの plane-triangle intersection

この問題に対する戦略も基本的には ray-polygon intersection と同じで，各独立した計算で同じ入力を保証するようにする。たとえば，ある 3 角形メッシュと平面の交線を求める時に，3 角形の辺上の点の計算をする場合を考える。図 2 に平面 $P$と 3 角形 $v_0 v_1 v_2$, $v_0 v_3 v_1$ が 交差する様子を示す。ここでの交線が $i_0 i_1$, $i_1 i_2$ で示されている。ここでは平面と 3 角形は co-planer ではなく，3 角形のどの辺も平面 $P$ 上にはなく，交線が定義できると仮定する。co-planer の場合も重要であるが，この場合は目的に依存した特別な処理が必要になることが多いので省く。

Figure 2: Plane-triangles intersection

 

Figure 3: Edge orientation

交点 $i_1$ の位置を求めることを考える。この時，辺としての表現は 2 通りある。

\[ \boldsymbol{e}_{v_0 \rightarrow v_2} &=& v_0 + t (v_2 - v_0) (1) \\

 \boldsymbol{e}_{v_1 \rightarrow v_0} &=&  v_2 + t (v_0 - v_2) (2)\]

図 3 には隣接する edge の向きが (a) のように対向する場合と (b) のように同一の場合がある。(b) で両方の矢印が逆を向く場合もあるがこれは同一の向きであり，(b) の場合に含めることができる。

associativity が保たれる場合には式 (1), (2) のどちらの表現で $i_1$ を計算しても問題がない。しかし，浮動小数点での計算では一般にわずかな違いがでる。そのため，この結果が同一の点であることを必要とするアルゴリズムでは問題が生じる。

そこで，このような辺上の点の計算では，この辺の $v_0$ と $v_1$ の順を一意に決めるようにする。一つの解決方法は点に total order をつけることである。例として C++ の std::map で使う点の比較用の functor の例を以下に示す。

// Simple example of a 3D point representation

struct Point3D {

    float x;

    float y;

    float z;

};

// Point3D comparison functor for the total ordering

struct comparePointOrder

{

    bool operator()(const Point3D& v0, const Point3D& v1) const

    {

        return (v0.x <  v1.x)

            || ((v0.x == v1.x) && (v0.y <  v1.y))

            || ((v0.y == v1.y) && (v0.z <  v1.z));

    }

};

この比較関数の考え方は数を位の値の大きい順に比較することと基本的には同じである。たとえば 2 桁の数，23 と 24 を比較する時，まずは 10 の位を比較して小さい方があればそれが小さい数である。10 の位が同じであれば，1 の位を比較して小さい方が小さい数になる。(ここで上記のプログラムでの同一判定を除いてしまうと比較は異なる意味になるので注意する。私はそのようなバグを書いてしまったことがある。)

辺上の点の交差点を計算する時，3 角形 $v_0 v_1 v_2$ と 3 角形 $v_0 v_3 v_1$ の各辺との計算時に上記の順が保たれるようにする。たとえば，$i_1$ の計算時には，3 角形 $v_0 v_1 v_2$ と平面との交差で $v_0 \rightarrow v_1$ が辺の入力になるのならば，3 角形 $v_0 v_3 v_1$ と平面との交差でも $v_0 \rightarrow v_1$ が入力になるようにする。計算を三角形ごとに行う場合，全体で一貫する順の辺は生成できないので，交差点の計算は各辺ごとに行う。

3 角形メッシュのデータ構造では，normal を一貫させるために図 2 (a) のように隣接する 3 角形の辺の順が保持されることが多い。しかし，平面との交差点の計算時には辺を図 2 (b)の向きにすることで，$i_1$ の位置を浮動小数点の binary 表現で一致させる。これは辺ごとの並列計算をする場合でも同じである。

このようにすると，点の lookup 時に上記の比較 functor と一緒に std::map を使うことも可能になる。これはシリアル計算でも有用であるが，並列計算時にはより効果を発揮する。

まとめ

ここでは数値計算の reproducibility をどうできるだけ保つかについて特に並列計算との兼ね合いを含めて述べた。3DDDA は優れたアルゴリズムであるが，この観点からは使いにくい。また，numerical reproducibility を保つために，入力の順を保つことを述べた。数学的には線分 AB と 線分 BA は区別しないことが多いが，numerical reproducibility に sensitive なアルゴリズムを使う場合には，線分 AB と 線分 BA は異なるものとして考えた方が良い。それに対処する一つの方法として点の total order を保つようにする Tip を述べた。

謝辞

英語版に有益なコメントを与えて下さった Andy Kopra 氏に感謝します。

参考文献

数値計算の reproducibility に関しては，例えば [1,2] を参照のこと。3DDDA については，[3] や Wikipedia の記事 [4] を参照のこと.

1. Nathalie Revol and Philippe Th{\'{e}}veny, "Numerical Reproducibility and Parallel Computations: Issues for Interval Algorithms", http://arxiv.org/abs/1312.3300, 2013
2. James Demmel and Hong Diep Nguyen, "Fast Reproducible Floating-Point Summation", In 21st IEEE Symposium on Computer Arithmetic, 2013
3. Fujimoto Akira and Takayuki Tanaka and Kansei Iwata, "ARTS: Accelerated Ray-Tracing System", IEEE CG & Applications, 148--157, 1986
4. Wikipedia, The Free Encyclopedia, "Digital differential analyzer: graphics algorithm", https://en.wikipedia.org/wiki/Digital_differential_analyzer_(graphics_algorithm), [Online; accessed 26-April-2021]